Степень с целым показателем корни натуральной степени

Как обычно — чтобы облегчить себе жизнь. Знание свойств степеней позволит тебе упрощать вычисления и считать быстрее, что пригодится и в жизни и на ОГЭ или ЕГЭ! Чтобы узнать все о степенях и научиться пользоваться свойствами степеней , читай эту статью.

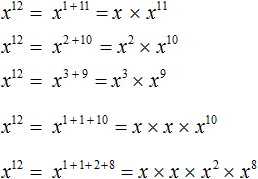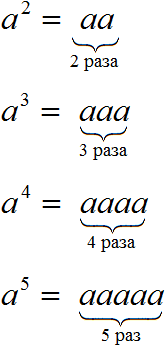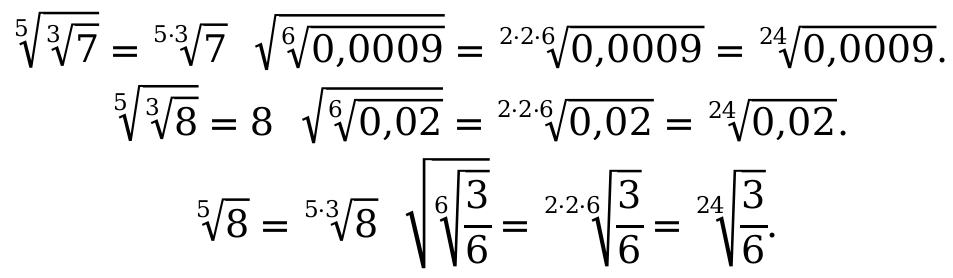
Степень с натуральным показателем

Регистрация Вход. Ответы Mail. Вопросы - лидеры.

Часто возникают задачи, в которых приходится находить произведение одинаковых множителей. Для упрощения записи таких выражений используется действие возведения в степень. Рассмотрим его подробно. В этом выражении. Следует отметить, что основанием степени с натуральным показателем может быть любое число, переменная или выражение. Переменные во второй или в третьей степени традиционно называются соответственно «квадратом» и «кубом» этих переменных.

• Свойства степени с рациональным показателем
• Понятие степени с целочисленным показателем включает в себя три определения.
• Тест соответствует учебнику "Алгебра.
• В статье рассмотрим свойства степеней с натуральным и рациональным показателями.

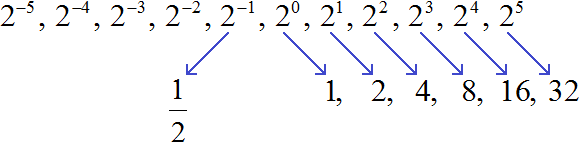
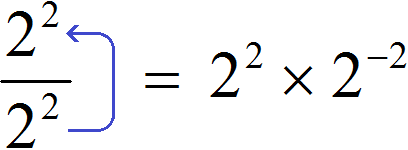
Как видно из первого примера, у вещественного корня чётной степени могут быть два значения положительное и отрицательное , и это затрудняет работу с такими корнями, не позволяя использовать их в арифметических вычислениях. Вещественные корни чётной степени из отрицательных чисел не существуют. Корни из комплексных чисел. Операция извлечения корня и алгоритмы её реализации появились в глубокой древности в связи с практическими потребностями геометрии и астрономии, см. Кроме приведённого выше, можно дать два равносильных определения корня [ 4 ] :. Вторая обратная операция, логарифмирование , находит показатель степени по известным основанию и результату.

Похожие статьи

• Поцелуй и секс тома и билла
• Фото пизд целок крупным планом
• Порно ломать целку онлайн
• Страстные поцелуи лесби онлайн